Table of Contents

1. Introduction
2. From DFAs in Circuits to NFAs with Pre-computation: The Big Shift
   • The v1 Approach (A Quick Look Back)
   • The v2 Vision: Separating Matching from Verification
3. Technique #1: Epsilon-Free NFA Generation
   • From Regex to an Initial NFA
   • The Problem with Epsilon Transitions
   • The Epsilon Elimination Algorithm
4. Technique #2: Mapping NFAs to Arithmetic Circuits
   • Flattening the NFA into a Transition Set
   • Off-Circuit Path Generation
   • In-Circuit Verification Process
   • Implementation Details and Performance
5. zk-Regex v2 Capabilities
   • Expanded Regex Support
   • Unsupported Features
   • Security Analysis: Trust Through Verification
   • Performance and Scalability
   • Proving System Agnostic Core
   • Simplified and Accurate Capture Groups
   • Current Limitations and Future Work
6. Applications and Broader Impact
7. Conclusion
   • Getting Started

1. Introduction

The ability to privately verify patterns in textual data is a fundamental building block for many secure applications. zk-Regex is a library that enables the generation of zero-knowledge proofs for regular expression matches, allowing a prover to demonstrate that a specific pattern exists within private text without revealing the text itself.

zk-Regex v1 was the first practical library of its kind to be used in production, successfully powering critical applications. These included:

• Bolstering sybil resistance mechanisms
• Enabling zk-p2p email proofs for financial transactions
• Facilitating secure email-based recovery for Ethereum accounts

The core strength of v1 lay in allowing users to selectively disclose specific strings and prove regex patterns within both email headers and bodies.

The v1 architecture, while powerful for its intended applications, was based on an approach—directly translating Deterministic Finite Automata (DFAs) into circuits—that involved inherent architectural trade-offs. This design choice was effective for its specific use cases but presented challenges in two main areas:

• Feature Support: It was difficult to support a broader set of standard regex syntax beyond what was required for its primary applications.
• Scalability: For the patterns it did support, the circuit's size and proving cost scaled directly with the complexity of the underlying DFA.

This article introduces zk-Regex v2, which builds upon the lessons from v1 to introduce a new architecture. The v2 model separates the complex task of regex matching from the in-circuit verification, enabling support for a much broader set of regex features with more efficient circuit construction. We will detail the architectural updates in v2, which enable more powerful and flexible ZK-based text processing, setting the stage for applications beyond regex, such as verifiable JSON parsing.

2. From DFAs in Circuits to NFAs with Pre-computation

The v1 Approach (A Quick Look Back)

The initial version of zk-Regex translated regular expressions into verifiable ZK circuits by directly embedding a Deterministic Finite Automaton (DFA) into an arithmetic circuit.

1. Regex Decomposition and DFA Construction:

The process began with a "decomposed regex" strategy, where a developer would split a pattern into a sequence of smaller regex "parts."

{
    "parts": [
        {
            "is_public": false,
            "regex_def": "email:"
        },
        {
            "is_public": true,
            "regex_def": "[a-z]+@[a-z]+.com"
        },
        {
            "is_public": false,
            "regex_def": "."
        }
    ]
}

Each regex_def was individually converted into a small DFA (hereafter a "part-DFA"). These part-DFAs were then linked sequentially by connecting the accepting states of one to the start state of the next, forming a single, larger DFA structure. The is_public flag marked the states corresponding to a given part for potential selective disclosure.

Each DFA is a Directed Acyclic Graph (DAG)—a network of nodes (states) connected by directed edges (transitions) with no cycles, meaning you can't traverse back to a previous state. The diagram below illustrates this process, showing how a complex regex is broken down into manageable parts, each converted to a DFA, and then combined into a final composed DFA:

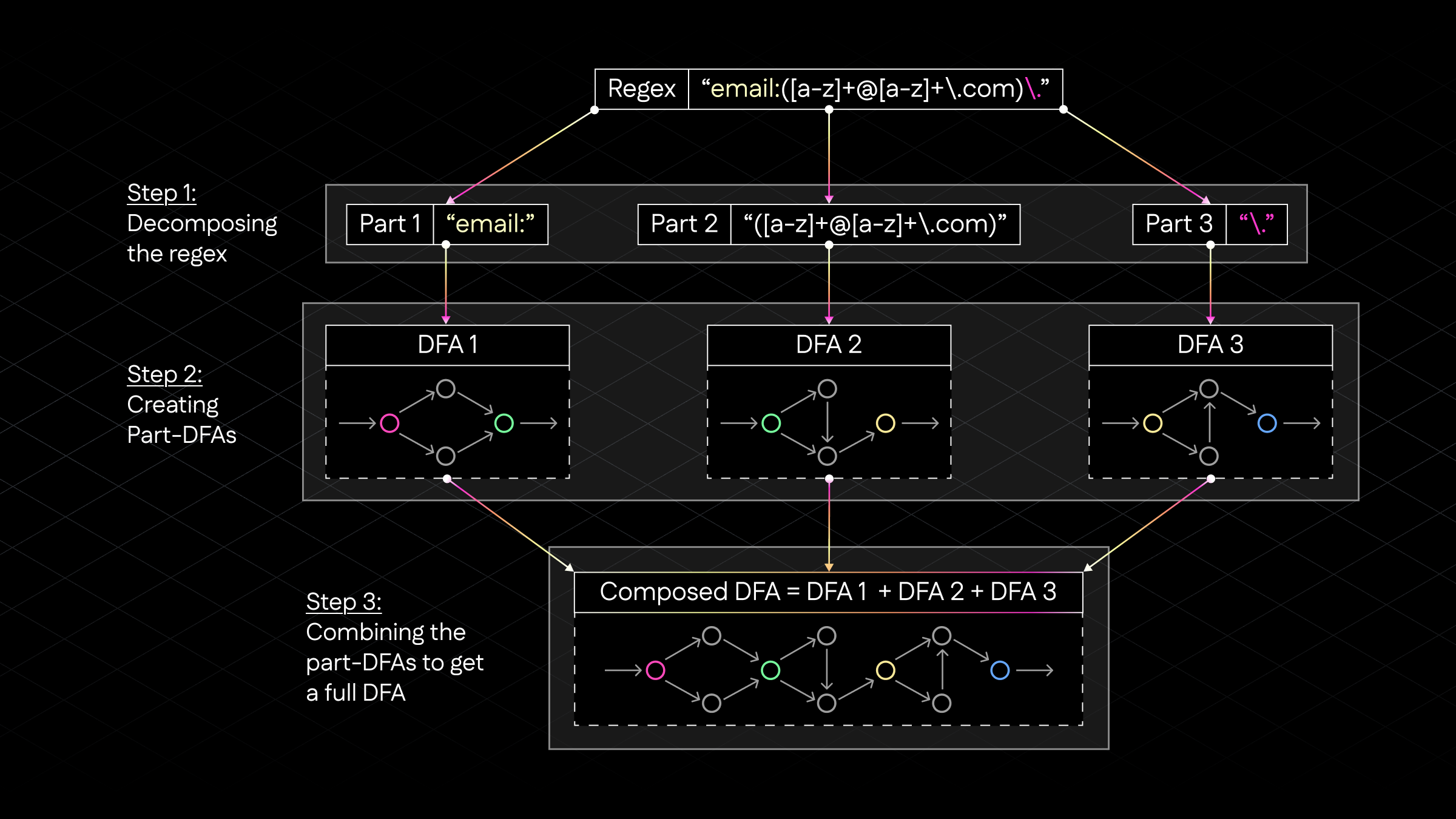
Figure 1: The v1 approach showing regex decomposition into parts, individual DFA construction, and final composition

2. Direct DFA-to-Circuit Translation:

The combined DFA was then translated into a Circom circuit that mirrored its state transition logic. For each input character, the circuit would evaluate the active DFA state, check the character against all possible transitions, and activate the next state. This required a large number of arithmetic components (IsEqual, AND, etc.) to encode the entire transition table, as shown in this simplified excerpt:

// ...
template BodyHashRegex(msg_bytes) {
    signal input msg[msg_bytes];
    signal output out;
    // ...
    signal states[num_bytes+1][35]; // Represents 35 DFA states over num_bytes
    // ...
    for (var i = 0; i < num_bytes; i++) {
        // ... (input character validation) ...
        // Example of transition logic from state 0 for character 13 ('\r')
        eq[0][i] = IsEqual();
        eq[0][i].in[0] <== in[i];
        eq[0][i].in[1] <== 13;
        and[0][i] = AND();
        and[0][i].a <== states[i][0]; // Is current state 0 active?
        and[0][i].b <== eq[0][i].out; // Is current char '\r'?
        // states_tmp[i+1][1] would be set based on and[0][i].out
        // ... many similar lines for all transitions from all states ...
        states[i+1][1] <== MultiOR(2)([states_tmp[i+1][1], from_zero_enabled[i] * and[0][i].out]); // Activate next state
    }
    // ...
    // Check if any accept state is reached
    component is_accepted = MultiOR(num_bytes+1);
    for (var i = 0; i <= num_bytes; i++) {
        is_accepted.in[i] <== states[i][34]; // State 34 is an accept state
    }
    out <== is_accepted.out;
    // ...
}

The number of pre-instantiated components in a full circuit demonstrated the resulting scale and constraint count.

3. Selective Disclosure (Capture Groups) in v1:

In regular expressions, a capture group is a sub-pattern enclosed in parentheses (...). Its purpose is to extract, or "capture," the portion of the input string that matches the pattern inside the parentheses. For example, in the regex email: ([a-z]+@[a-z]+\.com), the parentheses create a capture group that extracts just the email address from a larger string like "email: test@example.com".

In v1, this concept was handled by tracking when the DFA traversal entered and exited the states corresponding to a part-DFA marked is_public: true. Input bytes processed within these state segments were conditionally outputted, effectively simulating the capture.

4. Architectural Considerations in v1:

The direct DFA-in-circuit approach was a successful design with several key characteristics:

• Circuit Complexity and Size: Directly encoding a DFA's transition table into arithmetic constraints meant that circuit size and proving cost scaled with both the number of states in the DFA (a function of regex complexity) and the length of the input text. This created practical limits on the size of the emails that could be processed, as large inputs led to circuits that were too large to prove efficiently.

• Regex Feature Support: The architecture was best suited for patterns that mapped cleanly to DFAs. This posed challenges for features with significant non-determinism, such as complex alternations (|) or unbounded, non-greedy repetitions (*?, +?), which can cause an explosion in the number of DFA states.

• Capture Group Composition: The strategy of joining part-DFAs was a practical method that required careful manual composition to ensure the resulting automaton was semantically equivalent to the complete regex.

The observations from v1's production use and these architectural considerations informed the design of the new architecture in zk-Regex v2.

The v2 Vision: Separating Matching from Verification

Building on the lessons learned from v1's production use, the v2 design is centered on Non-deterministic Finite Automata (NFAs) and a separation of concerns: perform complex regex matching off-circuit, and use the circuit only for efficient verification.

The architectural comparison between v1 and v2 is illustrated in the diagram below, which clearly shows the fundamental shift from in-circuit simulation to off-circuit matching with in-circuit verification:

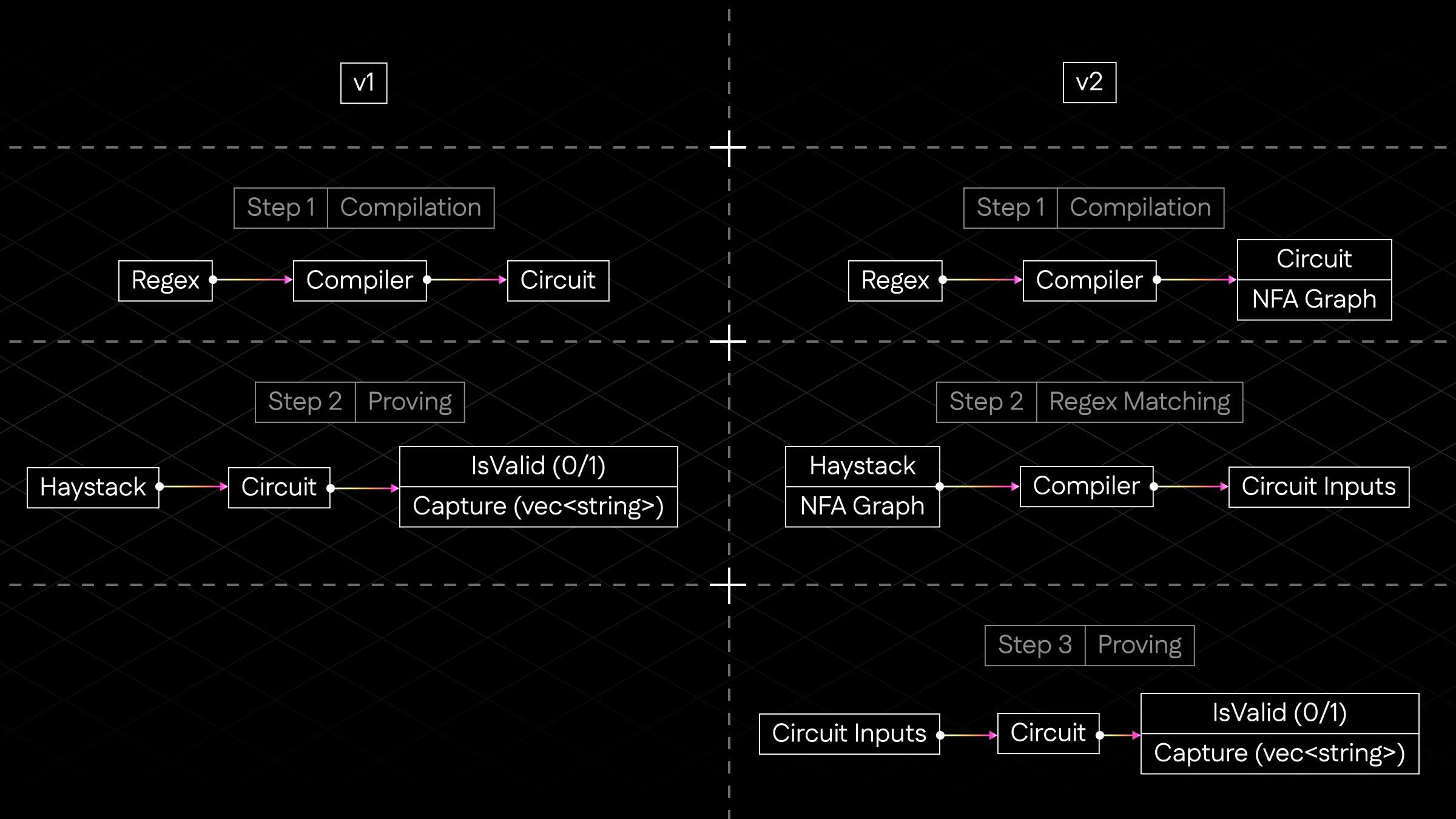
Figure 2: Architectural comparison showing v1's in-circuit DFA simulation versus v2's off-circuit NFA matching with in-circuit verification

v1 Architecture Steps:

• Step 1 - Compilation: Converts the regex directly into a circuit that embeds the full DFA transition logic. The circuit contains all possible state transitions and must simulate the entire automaton execution.

• Step 2 - Proving: Takes the haystack (input text) and runs it through the circuit, which simultaneously matches the regex pattern and generates the proof. All regex processing happens inside the ZK circuit.

v2 Architecture Steps:

• Step 1 - Compilation: Converts the regex into both a circuit (for verification) and an NFA graph (for matching). The circuit only contains transition validation rules, not the full execution logic.

• Step 2 - Regex Matching: Uses the NFA graph to find matches in the haystack off-circuit. Generates a traversal path (sequence of state transitions) and prepares circuit inputs containing only the matched segment and its path.

• Step 3 - Proving: The circuit verifies the provided traversal path against its embedded NFA rules. No regex execution occurs in-circuit—only validation of the pre-computed path.

1. Adopting Non-deterministic Finite Automata (NFAs):

The switch to NFAs as the foundational automaton was driven by several advantages:

• Compactness: NFAs are often significantly more compact than their DFA equivalents for regexes involving alternations, repetitions, or optional quantifiers.
• Robust NFA Construction: v2 uses Rust's mature regex_automata library. This provides optimized and well-tested NFA representations generated using a variant of Thompson's construction, which produces NFAs that are structurally aligned with the original regex pattern.
• Native Capture Group Support: The NFAs produced by regex_automata use special epsilon transitions (state transitions that do not consume input characters) to natively mark the entry and exit points of capture groups. This is a more integrated solution than v1's part-DFA stitching and allows a single, cohesive NFA to represent the entire pattern.

2. The Core Architectural Change:

The primary shift in v2 is the decoupling of the regex matching and ZK verification operations.

• Off-Circuit Path Finding: The process of finding a match (the "needle") in an input string (the "haystack") now occurs entirely outside the ZK circuit. This matching process traverses the NFA to find a "traversal path"—a sequence of valid state transitions, (current_state, input_byte, next_state), that consumes a segment of the haystack and ends in an NFA accept state.

• In-Circuit Verification: The ZK circuit's role is simplified to verification. It takes the pre-computed traversal path and the matched haystack segment as private inputs and checks them against a hardcoded representation of the NFA's transition rules. The circuit verifies:

  1. The path starts at a valid NFA start state.
  2. Each transition in the path is valid according to the NFA's rules.
  3. The path is contiguous (the next_state of one step is the current_state of the next).
  4. The path terminates in a valid NFA accept state.

Any tampering with the haystack or the claimed path will cause the in-circuit checks to fail.

3. Architectural Advantages:

This new design provides several key benefits:

• Reduced Circuit Complexity: By moving the complex matching logic off-circuit, the ZK circuits become simpler. They no longer simulate the automaton's execution but instead verify a linear sequence of transitions against a fixed set of rules. This generally results in fewer constraints and faster proving times.
• Expanded Regex Feature Support: Because the regex matching is performed by a standard, full-featured regex engine off-circuit, v2 can support a much wider range of regex syntax. The circuit only needs to verify the resulting path, regardless of how complex the off-circuit matching logic was.
• Targeted Matching: The off-circuit process identifies the specific substring that matches the regex, and only this segment and its corresponding traversal path are passed to the circuit, making proof generation more efficient for matches within large documents.
• Improved Modularity: The core NFA processing is proving-system agnostic. The final step translates this intermediate representation into circuit-specific code (e.g., for Circom or Noir), making the system more flexible and easier to maintain.

This separation of matching from verification is the foundation of zk-Regex v2's improved capabilities.

3. Technique #1: Epsilon-Free NFA Generation

To make NFA verification efficient within a ZK circuit, the automaton must be transformed into an equivalent one that does not use epsilon transitions. This section describes this transformation process.

From Regex to an Initial NFA

The process starts by constructing a Non-deterministic Finite Automaton (NFA) from the input regex string. For this, zk-Regex v2 uses Rust's regex_automata library. This approach provides two main benefits:

• Optimized Construction: The library uses a variant of Thompson's NFA construction, which produces NFAs that are structurally aligned with the regex and are often more compact than their DFA equivalents.
• Native Capture Groups: The generated NFAs use special epsilon transitions (via the State::Capture enum variant) to mark the boundaries of capture groups. This provides a single, integrated automaton with precise capture group information, avoiding the manual and fragile composition of part-DFAs used in v1.

The output of this stage is an NFA that correctly represents the regex but contains epsilon transitions, which are incompatible with direct circuit verification.

The Problem with Epsilon Transitions

An epsilon (ε) transition allows an NFA to change its state without consuming an input character. In standard automata theory, they are used to model features like alternations (|), repetitions (*, +), and capture groups.

However, epsilon transitions are problematic for circuit-based verification for two main reasons:

1. Complexity of Representing "Invisible" Steps: Modeling a transition that does not consume a byte is non-trivial in a fixed arithmetic circuit. It would require complex conditional logic to handle variable step types (byte-based vs. epsilon-based), increasing circuit size and complexity.

2. Difficulty Verifying "Gapped" Paths: A traversal path containing epsilon transitions would have "gaps" in the sequence of consumed bytes. The circuit would need to prove that these gaps correspond precisely to a valid sequence of epsilon transitions, which is complex and costly to implement with arithmetic constraints.

To resolve these issues, the epsilon transitions must be removed from the NFA before it is used to generate the circuit.

The Epsilon Elimination Algorithm

The solution is an algorithm that transforms the initial NFA into an equivalent one that is free of epsilon transitions, while preserving the original matching logic and capture group semantics.

The transformation process is illustrated in the diagram below, showing how an NFA with epsilon transitions is converted to an equivalent epsilon-free version:

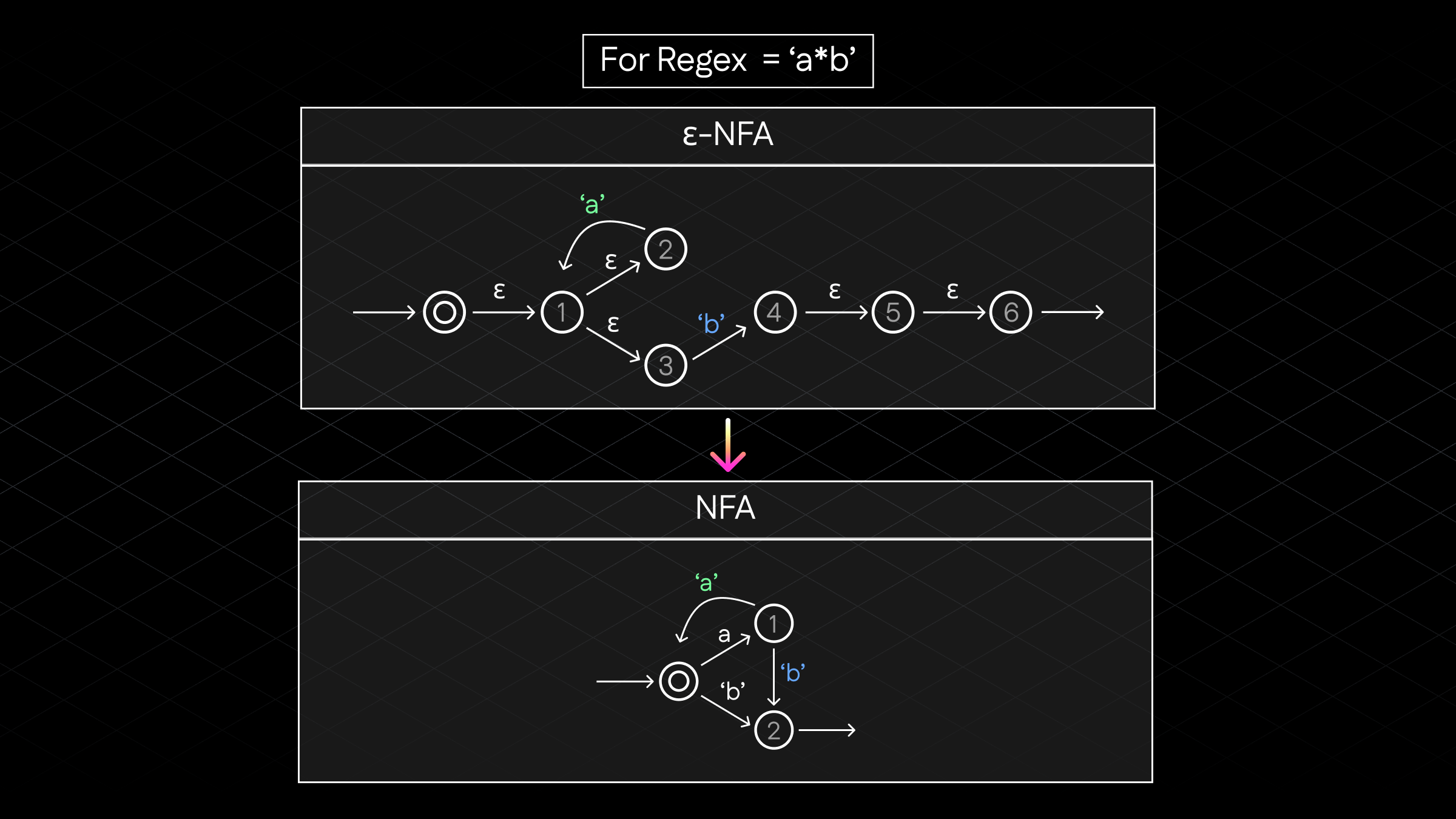
Figure 3: The epsilon elimination algorithm showing the transformation from an NFA with epsilon transitions to an equivalent epsilon-free NFA, with capture group markers preserved on byte-consuming transitions

The key assumption is that any meaningful capture group to be extracted must consume at least one byte.

The algorithm consists of the following stages:

1. Compute Epsilon Closures: For each state S, find its "epsilon closure" — the set of all states reachable from S using only epsilon transitions. This process also records any capture group events (start/end markers) and accept states encountered along these paths.

2. Rewire Transitions: Iterate through each state S. For each state R in the epsilon closure of S, if R has an outgoing byte transition R --byte--> T, create a new direct transition S --byte--> T. This new transition effectively bypasses the epsilon-only path from S to R.

3. Preserve Capture Group Semantics: When a new direct transition S --byte--> T is created, capture group markers from the bypassed epsilon path must be transferred to it. The logic associates these markers with the byte-consuming transition that forms the capture boundary:

   • Start Captures: Capture group start markers found on the epsilon path from S to R are attached to the new S --byte--> T transition. This marks the start of a capture group with the consumption of that specific byte.
   • End Captures: Capture group end markers found in the epsilon closure of the target state T are attached to the new S --byte--> T transition. This ties the end of a capture to the consumption of the byte that leads to T. This two-sided collection (pre-byte for starts, post-byte-target for ends) correctly delimits the captured substring in the final epsilon-free NFA.

4. Update Start and Accept States: The set of start and accept states is updated to reflect the new epsilon-free structure. For example, if any state S has an epsilon closure containing an accept state, S itself becomes an accept state.

5. Prune Unreachable States: After all epsilon transitions are removed, a graph traversal is performed from the new start states to identify and remove any states that are no longer reachable.

The output is an NFA that is behaviorally equivalent to the original but has no epsilon transitions. Every state change is tied to the consumption of an input byte, and all capture group information is preserved on these byte-based transitions. This structure is suitable for translation into an arithmetic circuit. This handling of capture groups is crucial for the system's correctness and, like any critical component in a ZK system, requires ongoing formal analysis and comprehensive fuzz testing to ensure its soundness. A formal specification of this algorithm will be provided in a future technical paper.

4. Technique #2: Mapping NFAs to Arithmetic Circuits

With an epsilon-free NFA prepared, the next step is to translate its logic into an arithmetic circuit friendly format. This section details how the NFA is represented within a circuit and how the off-circuit matching process interacts with the in-circuit verification.

Flattening the NFA into a Transition Set

An epsilon-free NFA is a graph structure. To use it in a circuit, we first "flatten" its rules into a structured list of all valid transitions. This process extracts three sets of data from the NFA:

1. A list of all valid start states.
2. A list of all valid accept states.
3. A complete set of all possible byte-based transitions, where each transition is a tuple containing (source_state, byte_range, destination_state) and any associated capture group events.

This set of transitions becomes the immutable ruleset embedded within the ZK circuit. The method for checking against this ruleset depends on the features of the target circuit DSL (Domain Specific Language).

• For Circom: Lacking native associative arrays, the circuit must iterate through the entire transition set for each byte of the claimed input path. It arithmetically confirms that the path's state change for that byte matches at least one of the valid transitions.
• For Noir: The transition set is encoded into a sparse array (a key-value map). A unique key is constructed from each (current_state, byte, next_state) tuple, which maps to a value encoding the transition's validity and its capture group data. This allows for more efficient, direct lookups.

The flattening process is illustrated in the diagram below, showing how the NFA graph structure is converted into a tabular format suitable for circuit verification:

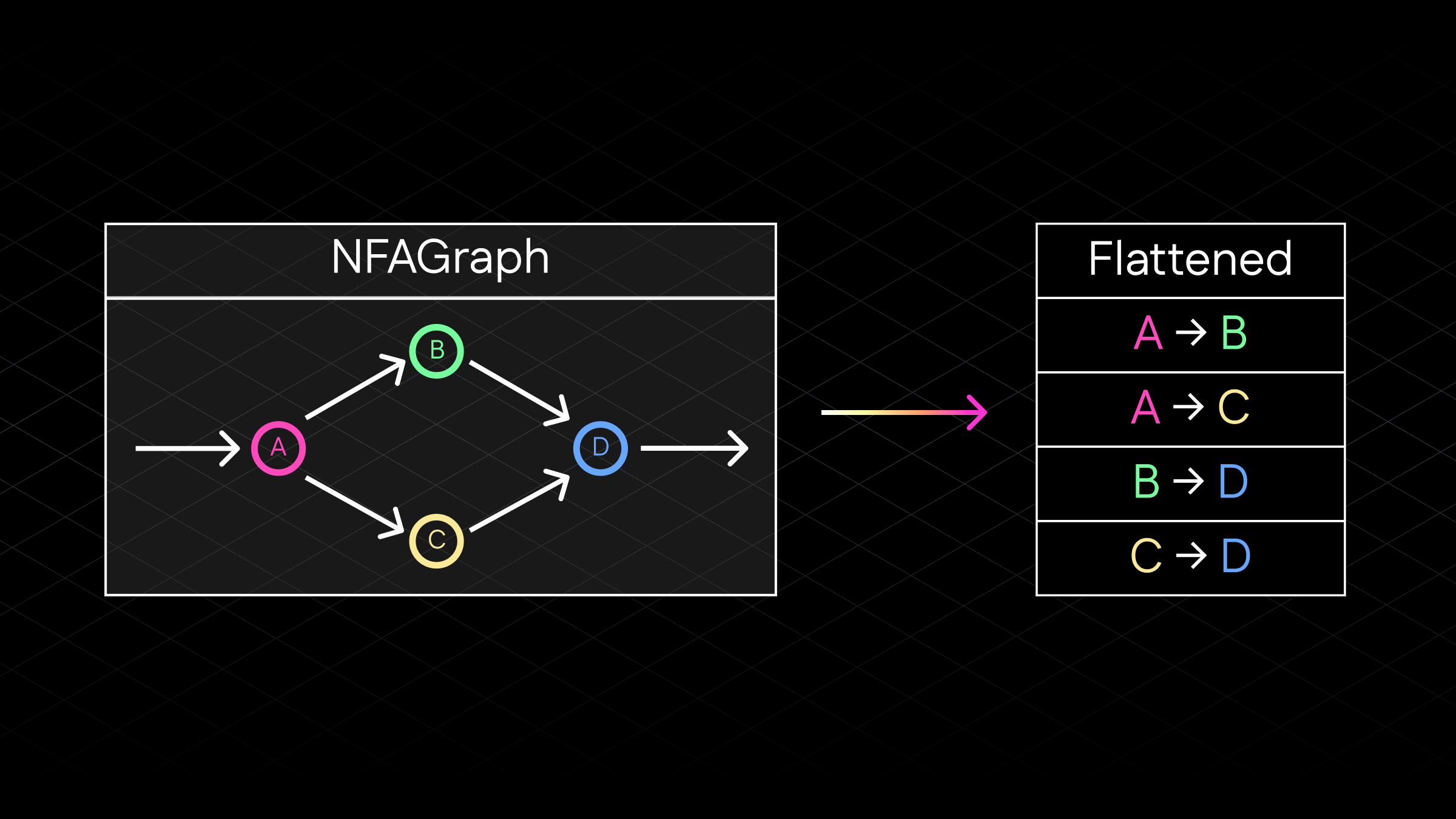
Figure 4: The NFA flattening process showing how the graph structure is converted into a structured transition table for circuit use

Off-Circuit Path Generation

The primary regex matching process occurs outside the ZK circuit. The prover's software takes the input string ("haystack") and uses the epsilon-free NFA to find a valid match ("needle"). If a match is found, this process generates a traversal path, which serves as the witness for the proof.

This path is a sequence of tuples, (current_state, byte_consumed, next_state, capture_group_events), that traces the NFA's execution through a contiguous segment of the haystack from a start state to an accept state. This traversal path and the corresponding substring from the haystack are then provided as private inputs to the circuit.

In-Circuit Verification Process

The ZK circuit's role is to verify, not execute, the match. It takes the private inputs from the prover and performs the following checks:

1. Valid Start State: It confirms the traversal path begins with a state present in the circuit's hardcoded list of valid start states.
2. Valid Transitions: For each step in the path, it verifies that the transition from current_state to next_state for the given byte_consumed is valid according to the embedded transition set. It also confirms that any claimed capture group activity for that step matches the rules for that specific transition.
3. Path Continuity: It enforces that the next_state of each step is identical to the current_state of the following step.
4. Valid Accept State: It confirms the final next_state in the path is a valid accept state.

Only if all these checks pass does the circuit accept the proof as valid and proceed to output the captured substrings. This architectural shift from in-circuit simulation (v1) to in-circuit verification of an execution trace is the primary source of v2's efficiency and expanded feature support.

Implementation Details and Performance

Encoding Strategy for Noir

Noir uses a sparse array data structure to efficiently store and lookup transition rules. A sparse array stores only non-zero values with their corresponding indices, making it ideal for NFAs where most state-to-state transitions don't exist.

The sparse array maps unique keys to transition data. For each valid transition (current_state, byte, next_state), a unique key is generated using a Random Linear Combination (RLC):

key = current_state + byte * 257 + next_state * 257^2

How the Key Works:

• Unique Positioning: Each component occupies a distinct "digit position" in base-257 arithmetic
• No Collisions: Since 257 > 255 (max byte value), no two different transitions can produce the same key
• Direct Lookup: The circuit can instantly check if a claimed transition exists by computing its key and looking it up in the sparse array

Example: For transition (state=5, byte=65, next_state=12):

key = 5 + 65 * 257 + 12 * 257^2 = 5 + 16,705 + 790,668 = 807,378

The sparse array value at this key contains the transition's validity flag and any associated capture group markers. This enables O(1) lookup time instead of iterating through all possible transitions, making Noir circuits significantly more efficient for complex regexes.

Performance Characteristics

The size of the transition set directly correlates with regex complexity (e.g., character classes, alternations, and repetitions increase the number of transitions). This has different performance implications for each DSL:

• Circom: Circuit complexity scales with O(match_length × total_transitions), as each input byte of the match requires an iteration through all possible transitions.
• Noir: Circuit complexity scales with O(match_length × lookup_cost), where lookup_cost is effectively constant due to the sparse array's direct key-based access.

For regexes with a large number of transitions, Noir's approach can result in significantly more efficient circuits.

5. zk-Regex v2 Capabilities

The v2 architecture provides several significant improvements over the previous version in regex support, security, performance, and modularity.

Expanded Regex Support

The primary advantage of the v2 architecture is its ability to support a much wider range of regular expression syntax. By moving the complex matching logic off-circuit, zk-Regex v2 can handle any pattern that the underlying regex_automata library can compile into an NFA.

This enables robust support for many standard regex features that were difficult or impossible to implement in v1's direct-to-circuit model, including:

• Non-greedy quantifiers (e.g., *?, +?).
• Complex alternations (|) and nested grouping.
• Unicode character classes and properties (e.g., \p{L}).

This approach also eliminates the need for the manual "decomposed regex" strategy from v1. Developers can now use a single, complete regex pattern, which is less error-prone and easier to maintain.

Unsupported Features

It is critical to note that zk-regex is constrained by the design of regex-automata, which intentionally omits certain features to guarantee linear-time matching performance. Consequently, zk-Regex v2 does not support:

• Lookarounds (e.g., (?=...), (?!...), (?<=...), (?<!...)).
• Backreferences (e.g., \1 or \k<name>).
• Other complex PCRE features like atomic groups.

Regex patterns containing these features will fail to compile.

Security Analysis: Trust Through Verification

The security of zk-Regex v2 relies on the verifiable integrity of the off-circuit computation. When a v2 circuit generates a valid proof, it provides strong cryptographic guarantees.

Soundness Guarantees

A valid proof guarantees that:

1. The claimed traversal path began at a valid NFA start state.
2. Every step in the path corresponds to a valid transition in the NFA ruleset embedded in the circuit.
3. The path properly terminated at a valid NFA accept state.

These checks make it computationally infeasible to generate a valid proof for a regex match that did not occur.

Attack Resistance

The design is resistant to several attack vectors:

• Invalid Transition Injection: An attacker cannot forge a traversal path with invalid steps, as every transition is checked against the immutable ruleset hardcoded in the circuit.
• Input Substitution: The circuit uses the bytes from the provided haystack to verify the traversal path, preventing a proof from being generated for one set of data and claimed against another.
• Capture Group Manipulation: Capture group boundaries are defined by the NFA structure and are verified at each step, preventing the contents of revealed substrings from being altered.

Completeness and Trust

• Completeness: If a regex match exists, a valid proof can be generated. The epsilon elimination process is designed to preserve the matching semantics of the original regex.
• Minimal Trust: The compiler operates deterministically and requires no trusted setup beyond that of the underlying proving system (e.g., Circom, Noir).

Performance and Scalability Characteristics

The v2 architecture changes how performance scales:

• Decoupled Complexity: Circuit size is no longer directly tied to the complexity of the regex pattern. Instead, it is primarily influenced by the maximum length of the match and the number of capture groups. A complex regex that produces a short match can result in a relatively small circuit - because the runtime cost being linear to the match length and not the regex complexity.
• Targeted Proving: The proving cost scales with the length of the matched substring, not the entire haystack, making it efficient for finding patterns in large documents.
• Efficient Resource Use: The CPU-intensive task of regex matching is handled off-circuit, reserving the more costly ZK circuit resources for the streamlined verification task.

While direct quantitative comparisons to v1 are difficult due to the architectural differences, this shift from in-circuit simulation to path verification leads to more efficient and scalable proofs for a wider class of problems.

Proving System Agnostic Core

The core logic of zk-Regex v2 is modular. The Rust-based compiler—responsible for parsing the regex, constructing the NFA, and performing epsilon elimination—is independent of any specific ZK proving system.

This compiler produces a standardized intermediate representation (NFAGraph). The final stage of code generation translates this representation into circuit code and input formats for a specific target like Circom or Noir. This design simplifies maintenance and makes it easier to add support for new proving systems in the future.

Simplified and Accurate Capture Groups

In v1, capture groups were handled by manually splitting a regex into parts. This approach was effective for its specific use cases but required careful implementation to ensure semantic consistency.

zk-Regex v2 handles capture groups more robustly:

• Capture groups are a native feature of the initial NFA generated by regex_automata.
• The epsilon elimination algorithm is designed to preserve the precise start and end boundaries of these groups, associating them with the correct byte-consuming transitions.
• The circuit verifies the claimed capture group events against the NFA's rules at each step of the traversal path.

This leads to capture group behavior that is more predictable and correctly aligned with standard regex engine semantics.

Current Limitations and Future Work

zk-Regex v2 is currently in an alpha stage of development. We encourage users and contributors to be aware of the following:

• Performance Benchmarking: Comprehensive performance data (e.g., constraint counts, proof generation times) is still being collected. The practical upper bounds on regex complexity and match length depend on the target proving system and user hardware. A detailed report will be released in a future publication.
• Formal Audits: The core algorithms have not yet been subjected to a formal external security audit or comprehensive fuzz testing. We strongly advise against using zk-Regex v2 in production environments until these milestones are complete.
• Feature Completeness: While the architecture theoretically supports any regex compilable by regex_automata, extensive testing across all syntax edge cases is ongoing.
• Deprecation of v1: With the release of this new architecture, zk-Regex v1 is officially deprecated and will no longer be maintained.

We are actively working on these areas and welcome community feedback.

6. Applications and Broader Impact

While zk-Regex v1 was primarily used for email processing, the v2 architecture expands its applicability to any domain requiring verifiable text pattern matching. The ability to efficiently prove regex matches on arbitrary text makes zk-Regex v2 a foundational primitive for applications requiring private data verification.

Potential use cases include:

• On-Chain Data Validation:

  • Smart contracts can use zk-Regex proofs to verify the format of off-chain data feeds (e.g., from oracles) before consumption, without bringing the full data on-chain.
  • Layer 2 solutions can validate user-submitted data against required formats before batching, ensuring compliance without exposing raw data.
  • On-chain registries or identity systems can enforce complex formatting rules in a privacy-preserving manner.

• Private Information Extraction:

  • Legal & Compliance: A user can prove a document contains a specific clause (e.g., "force majeure") or identifier without revealing the rest of the sensitive document.
  • Financial Analysis: A user can prove a financial report contains specific keywords or numerical patterns without disclosing the entire report to a verifier.
  • Research: Academics can prove the existence of specific data patterns in licensed datasets without sharing the raw data itself.

• Privacy-Preserving Content Moderation:

  • Users can prove that a message does not contain patterns matching a list of prohibited content, allowing it to pass through a gateway without the gateway reading the message.
  • Platforms can allow users to prove content meets certain community guidelines before upload, maintaining user privacy.

• Verifiable Credentials and Attestations:

  • An individual can prove that a digital ID contains an attribute matching a specific format (e.g., date_of_birth: YYYY-MM-DD or country_code: [A-Z]{2}) without revealing the attribute's value.
  • Organizations can issue attestations, and recipients can verify specific, regex-defined parts of them without needing access to the full data.

• Decentralized Information Markets:

  • Users can prove they possess information matching a search query (expressed as a regex) without revealing the information itself, facilitating privacy-preserving data markets.

The common thread is the ability to make credible assertions about textual data while preserving the confidentiality of the data itself. zk-Regex v2 provides a robust, flexible, and efficient toolkit to build these capabilities across diverse domains.

7. Conclusion

zk-Regex v2 introduces a new architecture for generating zero-knowledge proofs of regular expression matches. By changing the core approach from direct in-circuit DFA simulation to off-circuit NFA matching and in-circuit path verification, v2 addresses the primary limitations of the previous version.

The main technical shifts are:

1. A pre-processing step that transforms the NFA into an equivalent, epsilon-free automaton while preserving capture group semantics.
2. An architecture that moves the complex pattern-matching logic off-circuit, using the ZK circuit only to verify a pre-computed traversal path.

These changes result in a more capable and flexible system with several key benefits:

• Broader Regex Support: The ability to support a wider range of standard regex syntax.
• Improved Scalability: Circuit size scales with the length of the matched text, not the complexity of the regex, making proofs for complex patterns more feasible.
• Accurate Capture Groups: A more robust and predictable mechanism for handling capture groups.
• Proving System Modularity: A core, system-agnostic compiler that can be adapted to target different ZK-DSLs.

As a foundational tool for verifiable text-pattern matching, zk-Regex v2 enables developers to build a wider range of applications that require private data verification.

Getting Started

We encourage the community to explore the zk-Regex v2 compiler. The primary entry point is the zk-regex-compiler CLI tool, with the following workflow:

1. Compile: Use the raw or decomposed command to compile a regex pattern into circuit code (Circom/Noir) and a reusable NFA graph file.
2. Generate Inputs: Use the generate-circuit-input command with the NFA graph and input text to create the private inputs for the prover.
3. Prove: Integrate the generated circuit and inputs into your project to create and verify proofs.

For detailed instructions and examples, please refer to the project's README.md.

(A detailed technical paper with a formal specification of the epsilon elimination algorithm and performance benchmarks will be published soon.)